6. Реальные газы и пары
6.1. Термические свойства реальных газов
6.1.1. Отличие реальных газов от идеальных
Реальные газы отличаются от своей модели — идеальных газов — тем, что их молекулы имеют конечные размеры и между ними действуют силы притяжения (при значительных расстояниях между молекулами) и отталкивания (при сближении молекул друг с другом). Характер изменения этих сил взаимодействия в зависимости от расстояния между центрами молекул r показан на рис.
6.1. На рис. 6.2 в Р,v- диаграмме представлена изотерма реального вещества 1-2-3-4 и изотерма идеального газа ав.
Физика 10 класс (Урок№20 — Уравнение состояния идеального газа. Газовые законы.)
Характер поведения изотермы реального вещества 1-2-3-4 (рис.6.2) можно частично объяснить характером изменения сил взаимодействия между молекулами (рис.6.1) в зависимости от расстояния между их центрами при изменении давления, считая, что на обоих рисунках линиям 1-2-3-4 соответствует одна и та же изотерма.
В точке 1 при малых давлениях расстояние между молекулами большое (очень), здесь действуют небольшие силы взаимного притяжения молекул. На участке 1-2 при увеличении давления газ сжимается, объем его уменьшается.
По мере увеличения давления и уменьшения объема молекулы сближаются, силы притяжения возрастают и достигают максимума в точке 2. Силы взаимного притяжения молекул обусловливают появление внутреннего давления, которое возрастает по мере сближения молекул и приводит к более интенсивному изменению объема газа. Действие сил притяжения молекул в точке 2 аналогично действию пружины, которая полностью растянута.
Далее, начиная с точки 2 и до 3 (рис.6.2), газ будет переходить в жидкую фазу, т.е. здесь одновременно существуют газовая и жидкая фазы при одинаковых давлениях и температурах. В отношении двух молекул это динамичный процесс сближения, о двух фазах здесь говорить нельзя (рис.6.1), в точке 2 был газ, а в точке 3 стала жидкость.
При этом силы взаимного притяжения молекул уменьшаются, и в точке 3, где весь газ вступил в жидкую фазу, силы притяжения уравновешиваются силами отталкивания (условная пружина находится в свободном состоянии, не сжата и не растянута).
Уменьшение объема на процессе 2-3 (рис 6.2), с одной стороны, обусловлено внутренним давлением, которое падает в среднем до нуля в точке 3, а с другой стороны, объясняется образованием жидкой фазы, т.е. по мере увеличения количества капелек жидкости в смеси уменьшается количество газа, для газа объем соответствует точке 2, а для жидкости — точке 3, в результате удельный объем смеси при фазовом переходе уменьшается от точки 2 до 3.
При дальнейшем увеличении давления (процесс 3-4 рис.6.1 и 6.2) сжимается только жидкая фаза, при этом расстояния между молекулами настолько малы, что преобладают силы отталкивания, т.к. на сжатие уже оказывает влияние собственный объем молекул, соизмеримый со свободным объемом жидкой фазы. Т.е. собственный объем молекул оказывает противоположное воздействие силам взаимного притяжения (условная пружина полностью сжата).
В результате этого воздействия дальнейшее увеличение давления не приводит к значительному уменьшению объема жидкой фазы, т.е. жидкость — плохо сжимаемая фаза вещества.
Уравнение состояния идеального газа | Физика 10 класс #33 | Инфоурок
Разница между идеальным и реальным газом
Исследователи выделяют модели газа идеального и реального. В чем их специфика?
Что представляет собой идеальный газ?
В науке распространена трактовка понятия «идеальный газ», соответствующая гипотетическому веществу (не существующему в реальности), свойства которого могут быть описаны посредством уравнения Клапейрона — Менделеева.
Под идеальным газом понимается математическая модель соответствующего вещества, которая характеризуется:
- возможностью пренебрежения потенциальной энергией, образующейся в процессе взаимодействия частиц газа — в сравнении с уровнем кинетической энергии данных частиц;
- крайне малым общим объемом составляющих газ частиц;
- очень малым присутствием или же отсутствием дистанционных сил притяжения частиц либо отталкивания их;
- очень малым временем взаимодействия частиц друг с другом.
к содержанию ^
Что представляет собой реальный газ?
Под реальным газом, в свою очередь, понимается вещество, которое не может быть описано уравнением Клапейрона — Менделеева. Так, молекулы, присутствующие в нем, взаимодействуют друг с другом, формируют некоторый объем.

Нужно отметить, что во многих случаях характеристики потенциальной энергии, формирующейся в ходе взаимодействия молекул реального газа, существенно ниже кинетической энергии. Вследствие чего соответствующие газы по своим свойствам приближаются к тем, что характеризуют идеальный газ.
Заметные различия между рассматриваемыми веществами начинают появляться, как правило, при повышении давления и снижении температуры.
Сравнение
Главное отличие идеального газа от реального заключается в том, что в модели первого вещества практически не учитывается объем молекул, а также энергия их взаимодействия. В реальном газе соответствующие показатели учитываются.
Вместе с тем при невысоком давлении и большой температуре реальный газ по своим свойствам близок к идеальному.
Определив, в чем разница между идеальным и реальным газом, зафиксируем выводы в таблице.
Идеальный и реальный газ.
Уравнение состояния идеального газа.
Идеальным называется газ, взаимодействие между молекулами которого пренебрежимо мало.
Реальный газ при достаточном разрежении близок по своим свойствам к идеальному. Идеальный газ одно из двух идеальных систем,
для которых можно строго вывести уравнение состояния.
Для всех других систем уравнения состояния получают эмпирически.
Рассмотрим идеальный газ, заключенный в сосуде. Молекулы газа непрерывно соударяются с его стенками, в результате чего оказывают давление на них.
Рассмотрим взаимодействие молекул с одной стенкой (рис.1.15.1).
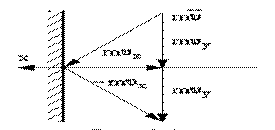
Вследствие хаотичности движения молекул давление газа на различные участки стенок сосуда одинаково. Давление газа на стенки определяется
р=(суммарная сила взаимодействия молекул со стенкой) / (площадь стенки)
Молекулы соударяются со стенкой упруго, т.е. отскакивают от стенки зеркально (углы падения и отражения равно). В результате взаимодействия с одной молекулой, массы т, движущейся со скоростью
, стенка, расположенная перпендикулярно оси х, получает импульс
.
Поскольку все направления движения равновероятны, за время dt со стенкой площадью
столкнется dN молекул, имеющих составляющую скорости
, dN=
, где
— число молекул в единице объема, имеющих скорости в интервале
. Величина
, п – концентрация молекул,
вероятность молекулам иметь скорость в указанном интервале.
Физика. МКТ: Идеальный газ. Центр онлайн-обучения «Фоксфорд»
Тогда сила соударения молекул, имеющих скорость в указанном интервале, с единичной площадкой стенки =
и полное давление всех молекул, соударяющихся с этой стенкой
. (1.15.1)
Выражение получено с учетом (1.14.11).
Это и есть уравнение состояния идеального газа:
. (1.15.2)
Это уравнение можно записать иначе, если учесть
,
,
( N — полное число молекул,
— число молей газа,
— число Авогадро, R — универсальная газовая постоянная)
. (1.15.3)
Идеальный и реальный газ | Газы.Молекулярно-кинетическая теория | Химия (видео 7)
Внутренняя энергия идеального газа.
Поскольку в идеальном газе отсутствуют силы взаимодействия между молекулами, то внутренняя энергия идеального газа представляет собой только кинетическую энергию молекул
, (1.15.4)
где i — число степеней свободы молекулы, которое равно 3 для одноатомной молекулы, 5 – для двухатомной, 6 – для многоатомной.
Теплоемкости и уравнение политропы идеального газа.
Из соотношений (1.13.5), (1.13.6), и (1.15.4) получим выражения для молярной теплоемкости при постоянном объеме и постоянном давлении идеального газа:
,
. (1.15.5)
Для получения уравнения политропы воспользуемся формулой (1.13.8).
Из уравнения состояния (1.15.3) получим
и
. Подставив эти значения в (1.13.8), получим
.
Проинтегрировав это равенство, будем иметь
. (1.15.6)
В частности, уравнение адиабатного процесса
(1.15.7)
Из соотношений (1.14.4), (1.12.7), (1.13.5) и (1.12.4) следует
.
Для идеального газа
. После интегрирования получим
. (1.15.8)
Реальный газ.
Уравнение Ван – дер – Вальса.
В реальных газах между молекулами существуют как силы притяжения, которые преобладают на далеких расстояниях, так и силы отталкивания, которые преобладают при сближении молекул. Действие сил отталкивания сводится к тому, что молекула не допускает проникновения в некоторый объем других молекул.
Следовательно, силы отталкивания характеризуются эффективным объемом молекулы. Наличие сил притяжения приводит к появлению дополнительного внутреннего давления.
Как уже говорилось, уравнение состояния реального газа нельзя получить аналитически.
Существует несколько различных уравнений, описывающих состояние реального газа. Все они получены эмпирически.
Чаще всего состояние реального газа описывают уравнением Ван – дер – Вальса, которое в достаточно широком диапазоне изменения параметров дает удовлетворительное согласие с экспериментом. Для моля реального газа оно имеет вид:
. (1.15.9)
Параметры а и b называются постоянными Ван – дер – Вальса.
Они зависят от рода газа.
Достоинство уравнения Ван – дер — Ваальса состоит не только в том, что оно описывает газовую фазу вещества в более широкой области температур и давления, но и в том, что оно описывает картину превращения газа в жидкость. Для объяснения этого факта рассмотрим зависимости давления от объема при постоянной температуре (изотермы).
Преобразуем уравнение Ван – дер — Ваальса для одного моля и запишем его по степеням объема
. (1.15.10)
Уравнение состояния стало кубическим относительно объёма, а число постоянных, являющихся его параметрами, стало равным трем. Как известно, кубическое уравнение имеет три корня.
Для уравнения Ван-дер-Ваальса имеют место три следующих случая: а) корни действительны; б) два корня мнимые и один корень действительный, в) три действительных корня тождественны.
На рис.1.15.2 схематически изображены изотермы газа Ван-дер-Ваальса для различных температур.
 |
| Рис.1.15.2. |
На части этих изотерм хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла.
В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма
при одинаковых значениях параметров p и
. Это соответствует существованию трёх действительных корней уравнения (1.15.10).
При повышении температуры волнообразный участок уменьшается и превращается в точку (точка К на рис.1.15.10). Эта точка называется критической, а значения
и
в этой точке называются критическими параметрами.
Критической точке соответствуют три совпадающих корня уравнения (1.15.10). При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями р(V).
Критические параметры
,
и
можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет точку перегиба. Из этого условия можно получить
|
. |
Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами
,
и
, величина которых зависит от свойств газа.
Обратимся теперь к экспериментальным кривым изотерм Ван-дер-Ваальса.
На рис.1.15.3 показан вид экспериментально полученных изотерм, характерный для многих веществ.
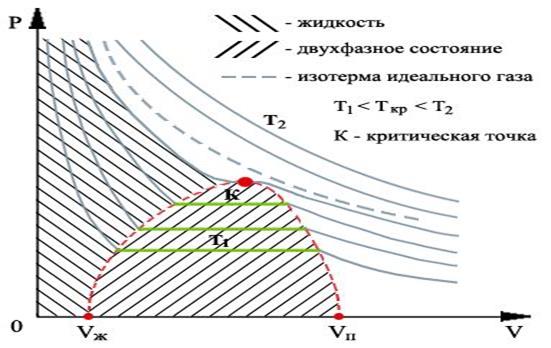 |
| Рис.1.15.3. |
На этих кривых виден горизонтальный участок, который заменяет немонотонный участок на теоретических изотермах газа Ван-дер-Ваальса (рис.1.15.2). Справа от горизонтального участка давление на экспериментальной изотерме монотонно растет с уменьшением объема, что соответствует сжатию реального газа при постоянной температуре.
Горизонтальный участок соответствует сжижению газа, которое при заданной температуре происходит при постоянном давлении. При этом существует двухфазная система жидкость-газ.
Наконец, слева от горизонтального участка, где изотерма вновь становится монотонно убывающей функцией
, весь газ превращается в жидкость. При этом давление очень резко растет с уменьшением объема.
Это связано с тем, что межмолекулярные расстояния становятся сравнимы с размерами молекул, что приводит к малой сжимаемости жидкостей.
Совокупность участков изотерм реального газа, соответствующих двухфазным системам жидкость-газ, образуют колоколообразную фигуру (см. рис.1.15.3), вершиной которой является критическая точка. выше критической вещество может существовать только в газообразном состоянии.
При температуре ниже критической, вещество может быть сжижено. Таким образом, на диаграмме можно указать три области значений параметров, при которых вещество может существовать только в газообразном, только в жидком состояниях и область, где жидкость и газ находятся в равновесии.
Например, критическая температура для гелия очень низкая — 5,2 К. Поэтому его сжижение связано с большими трудностями. В отличие от гелия, водорода, кислорода и азота, чьи критические температуры достаточно низкие (поэтому в основном они существуют в газообразном состоянии), такие вещества как вода и ртуть (критические температуры 647 К и 1820 К соответственно) существуют как в жидком, так и в газообразном состояниях при комнатных температурах.
Поэтому исчезает различие понятий "газ" и "пар".При температурах
Внутренняя энергия реального газа.
Для нахождения внутренней энергии газа Ван-дер-Ваальса, воспользуемся следующим приемом. Пусть над газом Ван-дер-Ваальса осуществляется процесс без теплообмена с окружающей средой.
Тогда изменение его внутренней энергии можно записать в виде
. (1.15.11)
При тех же условиях изменение внутренней энергии идеального газа можно было бы рассчитать по формуле
. (1.15.12)
Сравнивая уравнения состояния моля идеального (1.15.3) и реального (1.15.9) газов, можем видеть
и
, что после подстановки в (1.15.12) дает
Первое слагаемое в правой части этого выражения согласно формуле (1.15.11) представляет собой изменение внутренней энергии газа Ван-дер-Ваальса. Отсюда следует:
.
Интегрирование этого выражения дает
.
Здесь произвольную константу интегрирования необходимо положить равной нулю, так как при
выражения для внутренних энергий газа Ван-дер-Ваальса и идеального газа должна совпадать:
.
Использование выражения (1.15.4) для внутренней энергии идеального газа позволяет записать формулу, для расчета внутренней энергии одного моля газа Ван- дер – Вальса
. (1.15.13)
Как следует из этого выражения, внутренняя энергия газа Ван-дер-Ваальса зависит не только от его температуры, как в случае с идеальным газом, но и от объема, занимаемого им. По этой причине, при осуществлении изотермических процессов в газе Ван-дер-Ваальса, будет изменяться его внутренняя энергия, а, следовательно, при таких процессах подведенная к газу теплота не будет равна совершенной им работе.
Если внутренняя энергия идеального газа определяется кинетической энергией его молекул, то для газа Ван-дер-Ваальса существенное значение имеет потенциальная энергия, обусловленная силами притяжения и отталкивания.
Идеальный газ и настоящий газ 2020
ИДЕАЛЬНЫЙ ГАЗ против РЕАЛЬНОГО ГАЗА
Состояние вещества — это жидкое, твердое вещество и газ, которые можно распознать по их ключевым характеристикам.
Твердые тела имеют сильный состав молекулярного притяжения, придающий им определенную форму и массу, жидкости принимают форму их контейнера, так как молекулы движутся, что соответствует друг другу, и газы рассеиваются на воздухе, так как молекулы свободно движутся. Характеристики газов очень различны.
Есть газы, которые достаточно сильны, чтобы реагировать с другим веществом, есть даже с очень сильным запахом, а некоторые могут растворяться в воде. Здесь мы сможем отметить некоторые различия между идеальным газом и реальным газом.
Поведение реальных газов очень сложно, а поведение идеальных газов намного проще. Поведение реального газа может быть более ощутимым, полностью понимая поведение идеального газа.
Этот идеальный газ можно рассматривать как «точечную массу». Это просто означает, что частица чрезвычайно мала, где ее масса почти равна нулю.
Следовательно, идеальная газовая частица не имеет объема, а настоящая частица газа имеет реальный объем, поскольку настоящие газы состоят из молекул или атомов, которые обычно занимают некоторое пространство, хотя они чрезвычайно малы. В идеальном газе столкновение или удар между частицами называют упругими.
Другими словами, во время столкновения частиц нет ни привлекательной, ни отталкивающей энергии. Поскольку отсутствует межчастичная энергия, кинетические силы останутся неизменными в молекулах газа.
Напротив, столкновения частиц в реальных газах называются неупругими.
Реальные газы состоят из частиц или молекул, которые могут очень сильно привлекать друг друга с расходованием силы отталкивания или силы притяжения, подобно водяному пару, аммиаку, диоксиду серы и т. Д.
Давление значительно больше в идеальном газе по сравнению с давлением реального газа, поскольку частицы не имеют сил притяжения, которые позволяют молекулам сдерживаться, когда они будут сталкиваться при ударе.
Следовательно, частицы сталкиваются с меньшей энергией. Различия, отличные между идеальными газами и реальными газами, могут быть наиболее отчетливо видны, когда давление будет высоким, эти молекулы газа велики, температура низкая, а когда молекулы газа вырывают сильные силы притяжения.
PV = nRT — уравнение идеального газа. Это уравнение важно в его способности связывать все основные свойства газов.
T обозначает температуру и всегда должен быть измерен в Kelvin. «N» означает количество родинок.
V — объем, который обычно измеряется в литрах. P обозначает давление, в котором его обычно измеряют в атмосферах (атм), но также можно измерять в паскалях.
R считается идеальной газовой постоянной, которая никогда не изменяется. С другой стороны, поскольку все реальные газы могут быть преобразованы в жидкости, голландский физик Йоханнес ван дер Ваальс придумал модифицированную версию уравнения идеального газа (PV = nRT):
(P + a / V2) (V — b) = nRT.
Значение «a» является постоянным, а также «b», и поэтому должно быть экспериментально определено для каждого газа.
1. Идентификационный газ не имеет определенного объема, а реальный газ имеет определенный объем.
2. Идентификационный газ не имеет массы, тогда как реальный газ имеет массу.
3. Коллизия идеальных частиц газа является упругой, а не упругой для реального газа.
4. Нет энергии, участвующей при столкновении частиц в идеальном газе.
Столкновение частиц в реальном газе притягивает энергию.
5.Препарат высок в идеальном газе по сравнению с реальным газом.
6. Идентификационный газ следует уравнению PV = nRT. Реальный газ следует уравнению (P + a / V2) (V — b) = nRT.