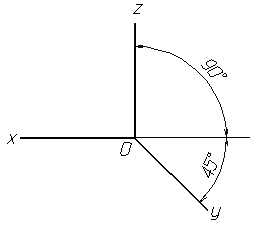Аксонометрические проекции
Настоящий стандарт устанавливает аксонометрические проекции, используемые в чертежах всех промышленных отраслей и строительства.
С прямыми углами проекции
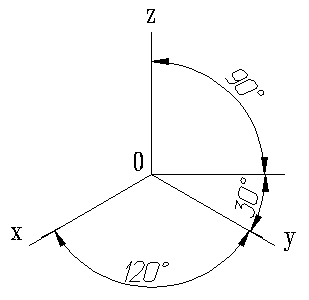
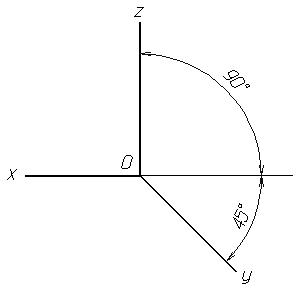
Рисунок 1. Расположение аксонометрических осей
квадратной изометрической проекции
Положение аксонометрических осей приведено на рис.1.
Показатель искажения по осям x, y, z равён 0.82.
Изометрическую проекцию для упрощения, в основном выполняют без искажения по осям x, y, z, т.е. приняв показатель искажения равным 1.
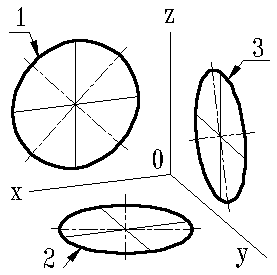
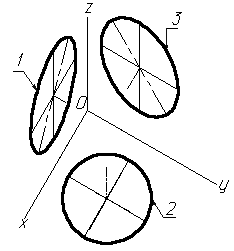
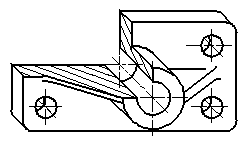
Окружности, лежащие в плоскостях, параллельных поверхностям проекций, проецируются на аксонометрическую поверхность проекций в эллипсы (рис.2)
Если аксонометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а небольшая ось — 0.71 диаметра окружности.
Если аксонометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось ось эллипсов 1, 2, 3 равна диаметру окружности, а небольшая — 0.58 диаметра окружности.
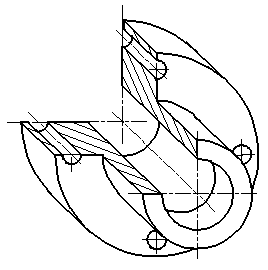
Пример изометрической проекции детали приведен на рис. 3.

Рисунок 2. Окружность в изометрии
1-эллипс (большая ось находится под углом 90 0 к оси y); 2-эллипс (большая ось находится под углом 90 0 к оси z); 3-эллипс (большая ось находится под углом 90 0 к оси x).
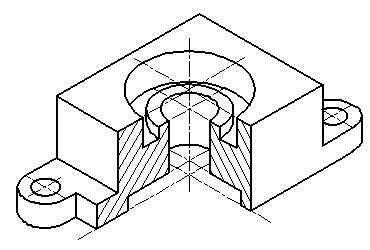
Рисунок 3. Изометрическое изображение детали
 |
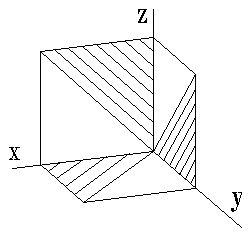 |
| Рисунок 16. Штриховка сечений в аксонометрических проекциях | |
При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии — параллельно измеряемому отрезку (рис. 17).
В разрезах на аксонометрических проекциях спицы маховиков и шкивов, жесткие ребра и такие элементы штрихуют (см. рис. 6).
При выполнении в аксонометрических проекциях зубчатых колес, планок, червяков и таких элементов разрешается использовать условности по ГОСТ 2.402—68.
В аксонометрических проекциях резьбу изображают по ГОСТ 2.311—68.
Разрешается изображать профиль резьбы полностью или частично, как показано на рис.
18.
В нужных случаях разрешается использовать прочие в теории обоснованные аксонометрические проекции.
Разница между изометрией и аксонометрией
Отображать разные геометрические предметы при помощи чертежей и при помощи графики с применением компьютеров можно с использованием принципов изометрии и аксонометрии. В чем характерность любого из них?
Что собой представляет аксонометрия?
Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех либо других геометрических предметов при помощи параллельных проекций.

Аксонометрия
Геометрический предмет в таком случае очень часто рисуется с применением конкретной системы координат — таким образом, чтобы та поверхность, на которую он проецируется, не соответствовала положению плоскости иных координат подобающей системы. Выходит, что предмет отображается в пространстве при помощи 2 проекций и смотрится объемно.
При этом потому, что поверхность отображения предмета не расположена строго параллельно какой-нибудь из осей системы координат, некоторые детали соответствующего отображения могут искажаться — по одному из 3 следующих принципов.
Во-первых, искажение элементов отображения предметов наблюдается по всем 3 осям, применяемым в системе, в равной величине.
В данном случае крепится изометрическая проекция предмета, или изометрия.
Второе, искажение элементов наблюдается лишь по 2 осям в равной величине.
В данном случае встречается диметрическая проекция.
Третье, искажение элементов может фиксироваться как различающееся по всем 3 осям. В данном случае встречается триметрическая проекция.
Рассмотрим, аналогичным образом, специфику первого типа искажений, формируемых в рамках аксонометрии.
Что собой представляет изометрия?
Итак, изометрия — это разновидность аксонометрии, которая встречается при прорисовке предмета например если искажение его элементов по всем 3 осям координат одинаковое.
Рассматриваемый вид аксонометрической проекции активно используется в промышленном планировании.
Он дает возможность хорошо смотреть те либо другие детали в рамках чертежа. Популярно применение изометрии и при разрабатывании компьютерных игр: при помощи соответствующего типа проекции становится потенциальным хорошо отображать трехмерные картинки.
Можно подчеркнуть, что в области современных промышленных разработок под изометрией в общем случае понимается прямоугольная проекция. Но иногда она может быть представлена и в косоугольной разновидности.
Сравнение
Основное отличие изометрии от аксонометрии состоит в том, что первый термин отвечает проекции, являющейся всего лишь одним из вариантов той, которая отмечается вторым термином. Изометрическая проекция, аналогичным образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии.
Отобразим более воочию то, в чем разница между изометрией и аксонометрией, в маленькой таблице.
Чем отличается изометрия от аксонометрии
Аксонометрия
Аксонометрия (от греч.
axcon — ось и metreo — измеряю) даёт наглядное изображение предмета на одной плоскости.
Изображение предмета в аксонометрии выходит путем параллельного проецирования его на одну поверхность проекций одновременно с осями прямоугольных координат, к которым данный предмет отнесен.
Коэффициенты искажения по осям в аксонометрии формируют отношением аксонометрических координатных отрезков к их настоящей величине при похожих единицах измерения.
Настоящие коэффициенты искажения обозначают:
В зависимости от сравнительной величины коэффициентов искажения по осям отличают 3 вида аксонометрии:
Изометрия — все три коэффициента искажения равны между собой: u=v=w.
Диметрия — два коэффициента искажения равны между собой и выделяются от 3-го u=v?w; v=w?u; u=w?v.
Триметрия — все три коэффициента искажения не равны между собой: u?v?w.
В зависимости от направления проецирования аксонометрические проекции делят на с прямыми углами (направление проецирования перпендикулярно плоскости аксонометрических проекций) и косоугольные (направление проецирования не перпендикулярно плоскости аксонометрических проекций).
С прямыми углами проекции
Изометрия
Положение аксонометрических осей приведено на рис.1.
Показатель искажения по осям x, y, z равён 0,82.
Изометрию для упрощения, в основном, выполняют без искажения по осям x, y, z, т. е. приняв показатель искажения равным 1.
Выстроенное аналогичным образом изображение будет побольше самого предмета в 1,22 раза, т.е. масштаб изображения будет М 1,22:1.
Окружности, лежащие в плоскостях, параллельных поверхностям проекций проецируются на аксонометрическую поверхность проекций в эллипсы (рис.2).
Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна 1,22, а небольшая ось — 0,71 диаметра окружности.
Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а небольшая ось — 0,58 диаметра окружности.
| Рис.2. Окружность в изометрии1 — эллипс (большая ось находится под углом 90° к оси у);2 — эллипс (большая ось находится под углом 90° к оси z);3 — эллипс (большая ось находится под углом 90° к оси х) |
Пример изометрической проекции детали приведен на рис.3.
Диметрия
Положение аксонометрических осей приведено на рис.4.
Показатель искажения по оси y равён 0,47, а по осям x и z — 0,94.
Диметрическую проекцию, в основном, выполняют без искажения по осям x и z и с показателем искажения 0,5 по оси y.
Аксонометрический масштаб будет М 1,06:1.
Окружности, лежащие в плоскостях, параллельных поверхностям проекций, проецируются на аксонометрическую поверхность проекций в эллипсы (рис.5).
Если диметрическую проекцию выполняют без искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а небольшая ось эллипса 1 — 0,95, эллипсов 2 и 3 — 0,35 диаметра окружности.
Если диметрическую проекцию выполняют с искажением по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а небольшая ось эллипса 1 — 0,9, эллипсов 2 и 3 — 0,33 диаметра окружности.
| Рис.5. Окружность в диметрии1 — эллипс (большая ось находится под углом 90° к оси у);2 — эллипс (большая ось находится под углом 90° к оси z);3 — эллипс (большая ось находится под углом 90° к оси х) |
Пример диметрической проекции детали приведен на рис.6.
Косоугольные проекции
Изометрия фронтальная
Положение аксонометрических осей приведено на рис.7.
| Рис.7. Оси фронтальной изометрии |
Разрешается использовать фронтальные изометрические проекции с наклонным углом оси у 30 и 60°.
Фронтальную изометрическую проекцию выполняют без искажения по осям x, y, z.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую поверхность в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной поверхностям проекций, — в эллипсы (рис.8). Большая ось эллипсов 2 и 3 равна 1,3, а небольшая ось — 0,54 диаметра окружности.
| Рис.8. Окружность в фронтальной изометрии1 — окружность;2 — эллипс (большая ось составляет с осью х угол 22°30?);3 — эллипс (большая ось составляет с осью z угол 22°30?) |
Пример фронтальной изометрической проекции детали приведен на рис.9.
| Рис.9. Деталь в фронтальной изометрии |
Изометрия горизонтальная
Положение аксонометрических осей приведено на рис.10.
| Рис.10. Оси горизонтальной изометрии |
Разрешается использовать горизонтальные изометрические проекции с наклонным углом оси y 45 и 60°, сохраняя угол между осями x и y 90°.
Горизонтальную изометрическую проекцию выполняют без искажения по осям x, y и z.
Окружности, лежащие в плоскостях, параллельных горизонтальной поверхности проекций, проецируются на аксонометрическую поверхность проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной поверхностям проекций — в эллипсы (рис.11). Большая ось эллипса 1 равна 1,37, а небольшая ось — 0,37 диаметра окружности.
Большая ось эллипса 3 равна 1,22, а небольшая ось — 0,71 диаметра окружности.
| Рис.11. Окружность в горизонтальной изометрии1 — эллипс (большая ось составляет с осью z угол 15°);2 — окружность;3 — эллипс (большая ось составляет с осью z угол 30°) |
Пример горизонтальной изометрической проекции приведен на рис.12.
| Рис.12. Деталь в горизонтальной изометрии |
Диметрия фронтальная
Положение аксонометрических осей приведено на рис.13.
Аксонометрия в Archicad, Перспектива в линиях в архикаде
| Рис.13. Оси фронтальной диметрии |
Разрешается использовать фронтальные диметрические проекции с наклонным углом оси у 30 и 60°.
Показатель искажения по оси y равён 0,5, а по осям x и z — 1.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую поверхность проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной поверхностям проекций, — в эллипсы (рис.14). Большая ось эллипсов 2 и 3 равна 1,07, а небольшая ось — 0,33 диаметра окружности.
| Рис.14. Окружность в фронтальной диметрии1 — окружность;2 — эллипс (большая ось составляет с осью х угол 7°14?);3 — эллипс (большая ось составляет с осью z угол 7°14?) |
Пример фронтальной диметрической проекции детали приведен на рис.15.
| Рис.15. Деталь в фронтальной диметрии |
Диметрия и изометрия

Диметрия собой представляет один из видов аксонометрической проекции.
Благодаря аксонометрии при одном объемном изображении можно рассматривать объект сразу в трех измерениях.
Потому как коэффициенты искажений всех размеров по 2-м осям такие же, эта проекция и стала называться диметрия.
Прямоугольная диметрия
При расположении оси Z’ вертикально, при этом оси Х’ и Y’ образовывают с горизонтального отрезка углы 7 градуса 10 минут и 41 градус 25 минут. В квадратной диметрии показатель искажения по оси Y как правило составит 0,47, а по осям Х и Z вдвое больше, другими словами 0,94.
Чтобы осущесвить построение приближенно аксонометрические оси обыкновенной диметрии, нужно принять, что tg 7 градусов 10 минут равён 1/8, а tg 41 градуса 25 минут равён 7/8.
Как построить диметрию
Для начала нужно нарисовать оси, чтобы изобразить предмета в диметрии. В любой квадратной диметрии углы, находящиеся между осями Х и Z, равны 97 градусов 10 минут, а между осями Y и Z — 131 градусов 25 минут и между Y и Х — 127 градусов 50 минут.
Теперь требуется нанести оси на ортогональные проекции изображаемого предмета, имея в виду подобранное положение предмета для вычерчивания в диметрической проекции. После того, как окончите перенос на рельефное ихображение больших размеров предмета, смело приступайте к чертежу несущественных элементов на поверхности предмета.
Необходимо запомнить, что окружности в каждой плоскости диметрии изображаются соответствующими эллипсами. В диметрической проекции без искажения по осям Х и Z большая ось нашего эллипса во всех 3-х плоскостях проекции как правило составит 1,06 диаметра нарисованной окружности.
А небольшая ось эллипса в плоскости ХОZ составляет 0,95 диаметра, а в плоскости ZОY и ХОY — 0,35 диаметра. В диметрической проекции с искажением по осям Х и Z большая ось эллипса равняется диаметру окружности во всех плоскостях.
В плоскости ХОZ небольшая ось эллипса составляет 0,9 диаметра, а плоскостях ZОY и ХОY равны 0,33 диаметра.
Дабы получить намного детальнее изображение, следует осуществить вырез через детали на диметрии.
Заштриховку при вычеркивании выреза следует наносить параллельно проведенной диагонали проекции подобранного квадрата на нужную поверхность.
Что такое изометрия
Изометрия считается одним из видов аксонометрической проекции, где расстояния единичных отрезков на всех 3-х осях одинаковые. Изометрическая проекция активно применяется в машиностроительных чертежах, чтобы отобразить внешний вид предметов, а еще в самых разных компьютерных играх.
В математике изометрия известна как переустройство метрического пространства, которое хранит расстояние.
Прямоугольная изометрия
В квадратной (ортогональной) изометрии аксонометрические оси делают между собой углы, которые равны 120 градусам. Ось Z находится вертикально.
Как нарисовать изометрию
Построение изометрии предмета позволяет построить получить наиболее выразительное представление о пространственных свойствах изображаемого объекта.
Прежде чем начать построение чертежа в изометрической проекции, нужно подобрать подобное размещение изображаемого предмета, чтобы были максимально заметны его пространственные свойства.
Теперь вам стоит определиться с видом изометрии, которую будете чертить. Есть два ее вида: прямоугольная и горизонтальная косоугольная.
Нарисуйте оси легкими тонкими линиями, чтобы изображение вышло по самому центру листа.
Как уже до недавнего времени говорилось, углы в прямоугольном виде изометрической проекции должны составлять 120 градусов.
Начните рисовать изометрию с собственно верхней поверхности изображения предмета.
От углов получившейся поверхности размещенной по горизонтали необходимо провести две вертикальные прямые и отложить на них подходящие линейные размеры предмета.
В изометрической проекции все линейные размеры по всех трем осям могут оставаться кратны единице.
Потом постепенно требуется объединить сделанные точки на вертикальных прямых. В результате выйдет внешний контур предмета.
Необходимо учесть, что при изображении любого предмета в изометрической проекции видимость криволинейных деталей будет обязательно искажаться. Окружность должна изображаться эллипсом.
Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равён диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.
Если изображаемый объект имеет невидимые пустоты ли непростые детали, попытайтесь выполнить заштриховку.
Она бывает самой обыкновенной либо ступенчатой, все будет зависеть трудности элементов.
Помните, что все построение должно исполнять строго с использованием чертежных инструментов.
Используйте несколько карандашей с различными видами твердости.
Виды аксонометрических проекций
Аксонометрические проекции в зависимости от направления проецирования делят на:
– косоугольные, когда направление проецирования не перпендикулярно плоскости аксонометрических проекций;
– с прямыми углами, когда направление проецирования перпендикулярно плоскости аксонометрических проекций.
В зависимости от сравнительной величины коэффициентов искажения по осям отличают 3 вида аксонометрии:
– изометрия — все три коэффициента искажения равны между собой (u = v = w);
– диметрия — два коэффициента искажения равны между собой и выделяются от 3-го (и не равно v = w или и= v не равно w);
– триметрия — все три коэффициента искажения не равны между собой (u не равно v не равно w).
Основное предложение аксонометрии сформулировано немецким геометром К. Польке: три произвольной длины отрезка прямых, лежащих на одном уровне и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных координатных осях от начала.
Согласно этой теореме любые три прямые в плоскости, исходящие из одной точки и не совпадающие между собой, можно принять за аксонометрические оси. Любые произвольной длины отрезки данных прямых, отложенные от точки их пересекания, можно принять за аксонометрические масштабы.
Данная система аксонометрических осей и масштабов считается параллельной проекцией некоторой квадратной системы координатных
осей и натуральных масштабов, т. е.
аксонометрические масштабы разрешено выдавать абсолютно произвольно, а коэффициенты искажения при этом связаны следующим соотношением: u2 + v2 = w2 = 2 + + ctg2(p, где ф — угол между направлением проецирования и плоскостью аксонометрических проекций (рисунок 156). Для квадратной аксонометрии, когда ф = 90°, это соотношение принимает вид и2 + v2 + w2 = 2 (1), т. е. сумма квадратов коэффициента искажения равна двум.
При прямоугольном проецировании может быть получена лишь одна изометрическая проекция и безграничное много диметрических и триметрических проекций. ГОСТ 2.317—69 учитывает использование в инженерной графике 2-ух прямоугольных аксонометрии: квадратной изометрии и квадратной диметрии с коэффициентами искажения и = w = 2v.
Прямоугольная изометрия
Прямоугольная изометрия отличается тем, что коэффициенты искажения составляют 0,82.
Их получают из соотношения (1).
Для квадратной изометрии из соотношения (1) приобретаем:
Зu2 = 2, или и = v — w = (2/3)1/2 = 0,82, т. е. отрезок координатной оси
длиной 100 мм в квадратной изометрии изобразится отрезком аксонометрической оси длиной 82 мм.
При практичных построениях пользоваться такими коэффициентами искажения не очень комфортно, благодаря этому ГОСТ 2.317—69 рекомендует пользоваться приведенными коэффициентами искажения:
Выстроенное аналогичным образом изображение будет побольше самого предмета в 1,22 раза, т. е. масштаб изображения в квадратной изометрии будет МА1,22: 1.
Аксонометрические оси в квадратной изометрии находятся под угол 120° друг к другу (рисунок 157). Изображение окружности в аксонометрии представляет интерес, особенно окружностей, принадлежащих координатным или им параллельным поверхностям.
В общем случае окружность проецируется в эллипс, если поверхность окружности находится под углом к плоскости проекции (см § 43). Поэтому, аксонометрией окружности будет эллипс.
Для построения квадратной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна аксонометрии той координатной оси, которая отсутствует в плоскости окружности.
Рисунок 157 — Аксонометрические оси в квадратной изометрии
В квадратной изометрии равные окружности, находящиеся в координатных плоскостях, проецируются в равные эллипсы (рисунок 158).
Размеры осей эллипсов при эксплуатации приведенных коэффициентов искажения равны: большая ось 2а= 1,22d, небольшая ось 2b = 0,71d, где d — диаметр изображаемой окружности.
Диаметры окружностей, параллельных координатным осям, проецируются частями, параллельными изометрическим осям, и изображаются равными диаметру окружности: l1=l2 =l3 = d, при этом l1||x; l2||y; l3||z.
Эллипс, как изометрию окружности, можно построить по восьми точкам, уменьшающим его большую и малую оси и проекции диаметров, параллельных координатным осям.
Рисунок 158 — Проецирование окружностей в квадратной изометрии
На практике инженерной графики эллипс, который является изометрией окружности, лежащей в координатной или ей параллельной плоскости, можно заменить четырехцентровым овалом, имеющим аналогичные оси: 2a = 1,22d и 2b = 0,71 d.
2 2 1 изометрия по чертежу
На рисунок 159 показано построение осей такого овала для изометрии окружности диаметра d (рисунок 159).
Рисунок 159 — Построение осей четырехцентрового овала для изометрии окружности
Для построения аксонометрии окружности, расположившейся в проецирующей плоскости или плоскости общего положения, необходимо выделить на окружности определённое число точек, построить аксонометрию данных точек и объединить их плавной кривой; получаем искомый эллипс— аксонометрию окружности (рисунок 160).
На окружности, расположившейся в в горизонтальном положении проецирующей плоскости, взято 8 точек (1,2,… 8).
Сама окружность отнесена к настоящей системе координат (рисунок 160, а).
Проводим оси эллипса квадратной изометрии и, применяя приведенные коэффициенты искажения, строим вторичную проекцию окружности 111,…, 511 по координатам х и у (рисунок 160, б).
Достраивая аксонометрические координатные ломаные для каждой из восьми точек, приобретаем их изометрию (11, 21, … 81). Объединяем плавной кривой изометрические проекции всех точек и приобретаем изометрию заданной окружности.
Рисунок 160 — Построение аксонометрии окружности, расположившейся в проецирующей плоскости или плоскости общего положения
Изображение геометрических поверхностей в квадратной изометрии рассмотрим на примере построения обычной с прямыми углами изометрии усеченного прямого кругового конуса (рисунок 161).
На комплексном чертеже изображен конус вращения, усеченный горизонтальной плоскостью уровня, находящейся на высоте z от нижнего основания, и профильной плоскостью уровня, дающей в сечении на поверхности конуса гиперболу с вершиной в точке А. Проекции гиперболы выстроены по индивидуальным ее точкам.
Отнесем конус к настоящей системе координат Oxyz. Построим проекции натуральных осей на комплексном чертеже и отдельно их изометрическую проекцию.
Построение изометрии начнем с построения эллипсов нижнего и верхнего оснований, которые считаются изометрическими проекциями окружностей оснований. Малые оси эллипсов совпадают с направлением изометрической оси ОZ(см.
рисунок 158). Большие оси эллипсов перпендикулярны малым.
Величины эллипсов осей определяются в зависимости от величины диаметра окружности (d — нижнего основания и d1— верхнего основания).
Потом возводят изометрию сечения конусообразной поверхности профильной плоскости уровня, которая пересекает основание по прямой, отстоящей от начала координат на величину XA и параллельной оси Оу.
Рисунок 161 — Типовая прямоугольная изометрия усеченного прямого кругового конуса
Изометрия точек гиперболы выстраивается по координатам, замеряемым на комплексном чертеже, и откладываем без изменения вдоль надлежащих изометрических осей, так как приведенные коэффициенты искажения и = v = w = 1.
Изометрические проекции точек гиперболы объединяем плавной кривой.
Построение изображения конуса завершается проведением очерковых образующих касательной к эллипсам оснований.
Незаметная часть эллипса нижнего основания проходит штриховой линией.
Прямоугольная диметрия
Прямоугольная диметрия отличается тем, что коэффициенты искажения, некоторые из выражения (1), и = w = 0,94, a v = 0,47. Формируют их так:
u2 =8/9; u = w = (8/9)1/2=0,94; v = 0,47.
Согластно ГОСТа 2.317—69 практические построения в квадратной диметрии необходимо выполнять пользуясь приведенными коэффициентами искажения: u = w=1и v = 0,5.
Расположение осей обычной с прямыми углами диметрии показано на рисунке 162.
Аксонометрический масштаб для квадратной диметрии будет МA1,06 : 1.
Рисунок 162 — Расположение осей обычной с прямыми углами диметрии
В квадратной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а небольшая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения.
Окружность, находящаяся в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а1 = 1,066d, небольшая ось — 2b1= 0,95d (рисунок 163).
Диаметры.
окружности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l1 = l2 = d; l = 0,5d, при этом || Ох; l2|| Оу; l3|| Oz.
Можно построить не считая перечисленных точек еще 4-ре точки, симметрические точкам, уменьшающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.
Рисунок 163 — Большая и небольшая оси в диметрии
Изображение геометрических поверхностей в квадратной диметрии рассмотрим на примере построения обычной с прямыми углами диметрии прямого кругового цилиндра.
На рисунке 164 приведен пример комплексного чертежа пустотелого цилиндра высотой Н c наружным d и внутренним d1диаметрами.
Цилиндр разместим в настоящую величину в настоящей системе координат Oxyz, относительно которой построим диметрическую его проекцию.
Как и в случае построения окружностей в изометрии, в диметрии также начинаем построение фигуры с эллипсов нижнего и верхнего оснований цилиндра, которые считаются изометрическими проекциями окружностей данных оснований.
Окружности основания размещены в плоскостях, параллельных горизонтальной поверхности проекций, благодаря этому, пользуясь ранееприведенными правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz.
Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов верхнего и нижнего оснований размещены на расстоянии Я.
Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров.
Выстроив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.
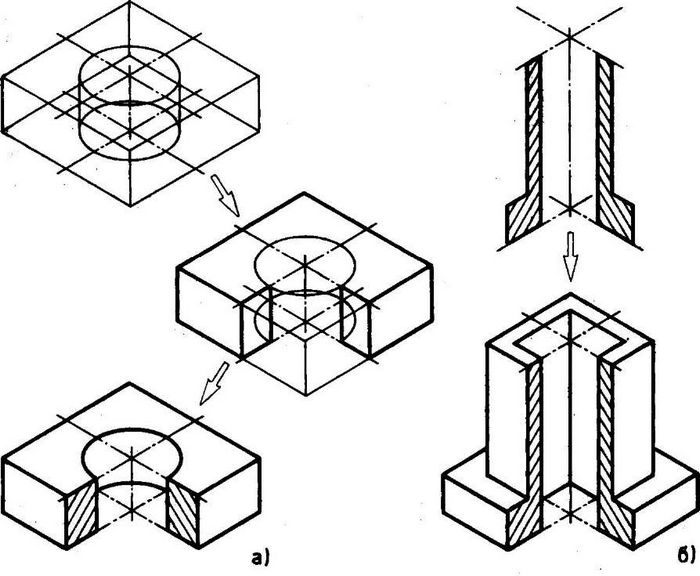
Для наглядности построим вырез четверти цилиндра, построение которого видно из рисунке 164.
Направление штриховки выреза подберём, как показано на рисунок 200. Незаметные линии покажем штриховыми линиями.
Для наглядности аналогичными линиями покажем линии вырезанной части цилиндра.
Видимые контурные линии наводят необходимой толщиной.
Рисунок 164 — Комплексный чертеж пустотелого цилиндра
Вопросы для самопроверки
1 Как образуется аксонометрический чертеж?
2 Каково дробление аксонометрических проекций в зависимости от направления проецирования?
3 Как находятся оси в квадратной диметрии?
4 Чему раны большая и небольшая оси в изометрии и диметрии?
Понятие об аксонометрии

Аксонометрическое черчение — изображение предмета, выполненное в аксонометрии (если перевести с др.греч.: аксон — ось, метрио — измеряю).
Метод аксонометрического проецирования есть ракурсное изображение предмета, параллельно спроецированное на изобразительную поверхность под конкретным к ней углом.
Аксонометрический чертеж — средство, позволяющее добиться большой наглядности, так как взгляд на объект в ракурсе с нижней либо верхней точки зрения дает возможность получить полное и емкое впечатление о его объемных и пространственных характеристиках.
С прямыми углами проекции — вид в передней части, сверху, с боковой стороны, плюс разрезы и сечения дают достаточную информацию о форме и размерах предмета, однако не дают наглядности. Суммарной информацией обладают аксонометрические проекции, т.е.
[AutoCAD 3D] Как построить виды, разрезы, изометрию детали в AutoCAD 2016
изображение предмета, получаемое его параллельным проецированием на одну поверхность одновременно с осями прямоугольных координат, к которым данный предмет отнесен.
Поверхность, на которую проецируется предмет, именуется картинной или аксонометрической.
Прямые линии и плоские фигуры предмета, параллельные между собой, изображаются такими и в аксонометрии.
Виды аксонометрии
Аксонометрические проекции именуют:
· прямоугольными — если направление проецирования перпендикулярно плоскости проецирования, г.е. угол между проецирующими прямыми и плоскостью изображения (картинная плоскость) равён 90°;
· косоугольными — если направление проецирования не перпендикулярно плоскости проецирования (или угол между проецирующими прямыми и плоскостью изображения отличен от прямого).
В общем случае любой предмет размещается в отношении к плоскости проецирования так, что размеры объекта несколько искажаются.
Отношение длины аксонометрической единицы к ее истинной величине именуется показателем искажения (критерием искажения).
Аксонометрические проекции называются:
· изометрическими — если коэффициенты искажения по всем осям равны между собой;
· диметрическими — если коэффициенты искажения равны по двум осям;
· триметрическими — если все коэффициенты искажения различны.
Прямоугольная изометрияне советуется для изображения объектов с планом квадратным или ближайшим к квадрату, так как в данном случае получаются невыгодные ракурсы предмета, грани которого изобразительно совпадают и визуально накладываются один на один.
Прямоугольная диметрия владеет замечательной воочиюстью, визуально мало искажает предмет, рекомендуется в архитектурной графике.
Косоугольная диметрия позволяет изображать предмет в большом диапазоне его пространственных ракурсов, мало искажает настоящий вид объекта, советуется для широкого использования в архитектурной графике.
Косоугольные изометрии дают возможность относительно не сложно воспринимать конструктивную, пластическую и пространственную структуры объекта, причем методы графического построения аксонометрии в сопоставлении с многообещающим чертежом просты и не слишком трудоемки.
Аксонометрические чертежи настолько условны, что визуально очень легко воспринимаются рядом с ортогональными проекциями. Фронтальную изометрию лучше применять для отдельно стоящего сооружения или здания (объемного объекта).
Горизонтальная изометрия советуется для объектов типа района, комплекса строений и аналогичных (площадные объекты). Очень часто применяемые виды аксонометрических проекций показаны на рис.
16.
Рекомендуется исполнять такие правила при выполнению аксонометрических чертежей.
Основа графического выполнения аксонометрического чертежа — его хорошее построение в линиях.
Карандашный аксонометрический чертеж должен быть чрезвычайно точным и выразительным, потому что он считается обязательной подосновой для последующего выполнения в технике линейной, тональной или цветной графики.
От качества и доскональной точности зависит красота линейной тушевой обводки, полнота и точность исполнения чертежа с использованием тона и цвета.
Не необходимо выбирать углы между осями ина глаз” и ограничивать построение лишь заметных граней формы в аксонометрической проекции.
Следует возводить как бы прозрачное изображение с видимыми и незаметными гранями формы.
Неукоснительно выполнять ключевые положения параллельного проецирования:
аксонометрические проекции параллельных прямых и плоскостей параллельны между собой;
« равные отрезки, принадлежащие параллельным прямым, проецируются в равные отрезки;
если точка делит отрезок в установленном отношении, .то ее аксонометрическая проекция делит аксонометрическую проекцию отрезка в том же отношении.
Построение ортогонального или аксонометрического чертежа основано на применении приемов, которые обобщенно носят наименование метода параллельного проецирования. Принцип этого метода построения: точка схода проецирующих прямых условно принимается как бесконечно удалённая, что и вызывает параллельность всех проецирующих прямых.
Если проецирующие прямые перпендикулярны к изобразительной плоскости, то в данном случае проецирование именуется методом ортогональных проекций (или методом Монжа). Если же проецирующие прямые сходятся в одну точку, то подобный прием называется метода центрального проецирования.
Конкретно данный метод является основой явления, носящего наименование «перспектива».
АРХИТЕКТУРНЫЙ РИСУНОК
Архитектурный рисунок как средство оформлении
Дата добавки: 2016-06-15; просмотров: 2847;
Как сделать аксонометрию

Во время проектирования на поверхность аксонометрических проекций П’ настоящей системы координат Oxyz выйдет аксонометрическая система координат O’x’y’z’, а проекция любой точки — аксонометрической проекцией или аксонометрией A’ (рисунок 1).
Если перенести с эпюра горизонтальную проекцию точки A? в новую систему, это будет так именуемая вторичная проекция и точка станет иметь аксонометрические координаты.Отношение аксонометрических координат к настоящим именуется критериями искажения по осям. Они обозначаются u, v, w, а величина углов между аксонометрическими осями — исходя из этого ?, ? и ?.
Есть самые разные виды аксонометрии.
В машиностроительном черчении чаще применяется прямоугольная аксонометрия.
В зависимости от величины критериев искажения u, v, w прямоугольная аксонометрия разделяется на виды:- изометрия — критерии искажения по всем трем осям равны между собой u=v=w.- диметрия — критерии искажения равны по двум осям u=w?v.
В большинстве случаев критерии искажения u, v, w имеют дробные значения, однако для упрощения построений применяются их приведенные значения. К примеру, в изометрии приведенные координаты равны настоящим.
Пример. Построить прямоугольную изометрическую проекцию призмы (рисунок 2).
Комплексный чертеж призмы задан в системе осей xyz, начало координат — точка О.
Постройте аксонометрические оси O’x’y’z’. Углы между осями ?, ?, ? равны 120? (рисунок 3).
В аксонометрических осях постройте вторичную проекцию призмы. Пускай начало координат точка O’ и ось z’ пройдёт через главную ось призмы z. Все размеры с комплексного чертежа перенесите на оси x’O’y’ без изменений, т.к. коэффициенты искажения по осям равны 1.
От точки O’ отложите отрезок О?1? и О?4? по оси x’. Отметьте точки 1’ и O’, а по оси y’ отложите отрезок О?А?.
Получите точки O’, A’.На эпюре отрезок 6?5? параллелен оси x?, значит, и отрезок 6’5’ проведите параллельно оси x’. Отложите на нем расстояние А?6? и А?5?.
Отметьте полученные точки 6’, 5’ и подобно постройте симметрические им точки 2’, 3’.
Проверьте положение точек 7’ и 8’, отложив размеры 7?А?.
Аналогичным образом, в аксонометрической проекции выстроена вторичная проекция основания призмы — 1’,2’,…8’. Из каждой точки проведите прямые, параллельные оси Z’.
На данных прямых отложите высоту каждой точки с фронтальной проекции призмы на эпюре.
От точки 1’ отложите отрезок 1?9?, а от точек 2’ и 6’ — отрезок 2?10?. От других точек 3’, 4’ и т.д.
отложите выделенную высоту h. Объединив все возведенные точки, получите аксонометрию этой призмы.
Аксонометрические проекции

По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым уютным для вас способом в разделе Контакты. Стоимость и потенциальные формы обучения (очно или на расстоянии) смотрите разделе Цены.
Детальнее о репетиторстве.
В большинстве случаев при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения.
Для построения подобных изображений используются проекции, именуемые аксонометрическими.
Способ аксонометрического проецирования заключается в том, что этот предмет одновременно с осями прямоугольных координат, к которым данная система относится в пространстве, параллельно проецируется на определенную поверхность ? (Рисунок 4.1).
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций ?, а еще коэффициенты искажения по ним.
При этом требуется обеспечить наглядность изображения и возможность делать определения положений и размеров предмета.
Как пример на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.
Тут буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ исходя из этого.
Если все три коэффициента равны между собой, то аксонометрическая проекция именуется изометрической, если равны между собой всего лишь два коэффициента, то проекция именуется диметрической, если же k?m?n, то проекция именуется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций ?
, то аксонометрическая проекция называется квадратной.
В другом случае, аксонометрическая проекция именуется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие с прямыми углами и косоугольные аксонометрические проекции:
- с прямыми углами изометрические и диметрические;
- косоугольные фронтально изометрические, в горизонтальном положении изометрические и фронтально диметрические;
Ниже приводятся параметры только трех очень часто применяемых В практических условиях аксонометрических проекций.
Любая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, размещенных в плоскостях, параллельных координатным поверхностям.
Для упрощения геометрических построений коэффициенты искажения по осям, в основном, округляются.
4.1. С прямыми углами проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
Рисунок 4.3 — Аксонометрические оси в квадратной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82.
Но с подобными значениями коэффициентов искажения работать не комфортно, благодаря этому, В практических условиях, применяются приведенные коэффициенты искажений.
Эта проекция в большинстве случаев делается без искажения, благодаря этому, приведенные коэффициенты искажений принимается k = m = n =1.
Окружности, лежащие в плоскостях, параллельных поверхностям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а небольшая — 0,71 диаметра создающей окружности D.
Большие оси эллипсов 1, 2 и 3 размещены под угол 90? к осям OY, OZ и OX, исходя из этого.
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.
Рисунок 4.4 — Изображение детали в квадратной изометрической проекции
4.1.2. Диметрическая проекция
Положение аксонометрических осей проходит на Рисунке 4.5.
Для построения угла, примерно равного 7?10?
, выстраивается прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, примерно равного 41?25? — катеты треугольника, исходя из этого, равны семи и восьми единицам длины.
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY — m=0,47. При округлении таких параметров принимается k=n=1 и m=0,5.
В данном случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 — 0,35D (D — диаметр окружности). На Рисунке 4.
5 большие оси эллипсов 1, 2 и 3 размещены под угол 90?
к осям OY, OZ и OX, исходя из этого.
Пример квадратной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.
Рисунок 4.5 — Аксонометрические оси в квадратной диметрической проекции
Рисунок 4.6 — Изображение детали в квадратной диметрической проекции
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на Рисунке 4.7. Разрешается использовать фронтальные диметрические проекции с наклонным углом к оси OY, равным 300 и 600.
Показатель искажения по оси OY равён m=0,5 а по осям OX и OZ — k=n=1.
Рисунок 4.7 — Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на поверхность XOZ без искажения.
Большие оси эллипсов 2 и 3 равны 1,07D, а небольшая ось — 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7?
14?
, а большая ось эллипса 3 составляет аналогичный угол с осью OZ.
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, эта деталь размещается поэтому, чтобы её окружности проецировались на поверхность XОZ без искажения.
Рисунок 4.8 — Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из данных окружностей разделяется на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые разделяют также вторую окружность. Потом через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересекания надлежащих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана только одна необходимая точка 1.
Рисунок 4.9 — Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ разделяется на несколько одинаковых частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (к примеру, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения.
Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 разделяется на то же число одинаковых частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, помноженным на показатель искажение (в нашем случае — 0,5).
4.4 Штриховка сечений
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в надлежащих координатных плоскостях, их стороны параллельны аксонометрическим осям (Рисунок 4.10: а — штриховка в квадратной изометрии; б — штриховка в косоугольной фронтальной диметрии).
а б Рисунок 4.10 — Варианты штриховки в аксонометрических проекциях
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым уютным для вас способом в разделе Контакты. Стоимость и потенциальные формы обучения (очно или на расстоянии) смотрите разделе Цены.
Детальнее о репетиторстве.
Аксонометрические проекции

Аксонометрические изображения повсеместно используются благодаря хорошей наглядности и простоте построений.
Слово «аксонометрия» если перевести с греческого значит измерение по осям.
Аксонометрический метод может комбинироваться и с параллельным, и с центральным проецированием при условиях, что предмет проецируется одновременно с координатной системой.
Сущность метода параллельного аксонометрического проецирования (рис.44) состоит в том, что предмет относят к некоторой системе координат и потом проецируют параллельными лучами на поверхность одновременно с координатной системой.
На рисунке показана точка А, отнесенная к системе прямоугольных координат xyz. Вектор S определяет направление проецирования на поверхность проекций П*.
Аксонометрическую проекцию А1* горизонтальной проекции точки А называют вторичной проекцией.
Искажение отрезков осей координат при их проецировании на П‘ отличается называющимся показателем искажения.
Показателем искажения именуется отношение длины проекции отрезка оси на картине к его истинной длине.
Так по оси x* показатель искажения составляет u=0*x*/0x, а по оси y* и z* исходя из этого ?=0*y*/0y и ?=0*z*/0z.
В зависимости от отношения коэффициентов искажения аксонометрические проекции могут быть:
Изометрическими, если коэффициенты искажения по всем трем осям равны между собой; в данном случае u=?=?;
Диметрическими, если коэффициенты искажения по двум любым осям равны между собой, а по третьей — разнится от первых 2-ух;
Триметрическими, если все три коэффициента искажения по осям различны.
Аксонометрические проекции отличаются также и по тому углу ?
, который образуется проецирующим лучом с плоскостью проекций. Если ??
900, то аксонометрическая проекция именуется косоугольной, а если ?= 900– квадратной.
Рассмотрев общие сведения об аксонометрических проекциях, можно создать такие выводы:
– аксонометрические чертежи обратимы;
– аксонометрическая и вторичная проекции точки вполне формируют её положение в пространстве.
Аксонометрические проекции обратимы, если известна аксонометрия трех основных направленностей измерений фигуры и коэффициенты искажения по этим направлениям.
Аксонометрические проекции фигуры являются её проекциями на плоскости произвольного положения при произвольно подобранном направлении проецирования.
Понятно возможно и обратное. На плоскости можно подобрать произвольное положение осей с произвольными аксонометрическими масштабами.
В пространстве всегда возможно подобное положение настоящей системы прямоугольных координат и подобный размер настоящего масштаба по осям, параллельной проекцией которых считается эта аксонометрическая система.
Главная ТЕОРЕМА АКСОНОМЕТРИИ
(теорема ПОЛЬКЕ)
Немецкий ученый Карл Польке (1810 -1876) сформулировал главную теорему аксонометрии:
Три отрезка прямых произвольной длины, лежащих на одном уровне и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на координатных осях от начала.
Согласно этой теореме, любые три прямые в плоскости, исходящие из одной точки и не совпадающие между собой, можно принять за аксонометрические оси.
Любые отрезки произвольной длинны на данных прямых, отложенные от точки их пересекания, можно принять за аксонометрические масштабы.
Данная система аксонометрических осей и масштабов считается параллельной проекцией некоторой квадратной системы координатных осей и натуральных масштабов.
На практике построения аксонометрических изображений в большинстве случаев используют лишь некоторые отдельные конфигурации направленностей аксонометрических осей и аксонометрических масштабов: прямоугольная изометрия и диметрия, косоугольная фронтальная диметрия, кабинетная проекция и др.
Согласно ГОСТ 2.317-69, из прямоугольных аксонометрических проекций лучше всего использовать с прямыми углами изометрию и диметрию.
Между коэффициентами искажения и углом ?, образованным направлением проецирования и картинной плоскостью, есть следующая зависимость:
В изометрии u=?=? и, поэтому, 3u2=2, откуда u=O2/3 ? 0,82.
Аналогичным образом, в квадратной изометрии размеры предмета по всем трем измерениям уменьшаются на 18 %.
ГОСТ рекомендует изометрическую проекцию строить без сокращения по осям координат, что отвечает увеличению изображения против оригинала в 1,22 раза.
При построении квадратной диметрической проекции уменьшение длин по оси y’ принимают вдвое больше, чем по двум иным, т.е. считают, что u=?, а ?=0,5u.
Тогда 2u2+(0,5u)2=2, откуда u2=8/9 и u?0,94, а ?=0,47.
В практичных построениях от подобных дробных коэффициентов в большинстве случаев отказываются, вводя масштаб увеличения, определяемый соотношением 1/0,94=1,06, и вот тогда коэффициенты искажения по осям x’ и z’ равны единице, а по оси y’ вдвое меньше ?=0,5.
Из косоугольных аксонометрических проекций ГОСТом рассчитано использование фронтальной и горизонтальной изометрии и фронтальной диметрии (последнюю ещё именуют кабинетной проекцией).
Аксонометрические проекции. Плоские фигуры в аксонометрии

? ПредыдущаяСтр 4 из 5Следующая ?
Аксонометрические проекции собой представляют наглядное и очень точное изображение предметов.
К аксонометрическим проекциям относится косоугольная фронтальнодиметрическая проекция и прямоугольная изометрическая проекция.
Слово ”аксонометрия” — греческое, в переводе значит измерение по осям, или измерение параллельно осям.
Аксонометрические проекции очень часто используют в качестве иллюстраций в учебных пособиях, разных руководствах, на плакатах.
Во фронтальнодиметрической (диметрии) ось ОХ располагают в горизонтальном положении, ось ОZ под угол 90° к оси ОХ, а ось ОY под угол 45° к горизонтальной линии.
В изометрической проекции (изометрии) ось ОZ размещена вертикально, а оси ОХ и ОY составляют с ней углы, равные 120о. На рис.
64 показаны положение осей, приемы построения осей, построение осей при выполнении технических рисунков.
Рис. 64.
Положение осей при построении аксонометрических проекций
“Диметрия” если перевести с греческого значит “двойное измерение”. В диметрии по осям ОХ и ОZ откладуют действительные размеры, а по оси ОY- меньше практически вдвое.
“Изометрия” если перевести с греческого значит “равные измерения”. В изометрии по осям ОХ, ОY, ОZ и линиям им параллельным откладуют действительные размеры.
Построение аксонометрических проекций начинают с изображения основания, т.е. плоских фигур, размещенных в одной из плоскостей. Рассмотрим сначала изображение плоских фигур в аксонометрии, так как знание приемов построения плоских фигур нужно для построения аксонометрических проекций геометрических тел.
Пример 1. Построение аксонометрических проекций равностороннего треугольника.
Треугольник находится на фронтальной плоскости (рис.
65).
Рис. 65.
Треугольник на фронтальной плоскости
По оси ОХ откладуют размер b по оси ОZ — высоту h, точки объединяют (для изометрии и диметрии).
Треугольник находится на горизонтальной поверхности (рис.
66).
Рис.
66. Треугольник на горизонтальной поверхности
По оси ОХ откладуют размер b, а по оси ОY- высоту h треугольника(в изометрии), в димертии по оси ОY- половину высоты треугольника.
Треугольник находится на профильной плоскости (рис. 67).
Рис.
67.
Треугольник на профильной плоскости
По оси ОY откладуют размер b в изометрии, в диметрии по оси ОY — половину размера b треугольника.
По оси ОZ откладуют h высоту треугольника.
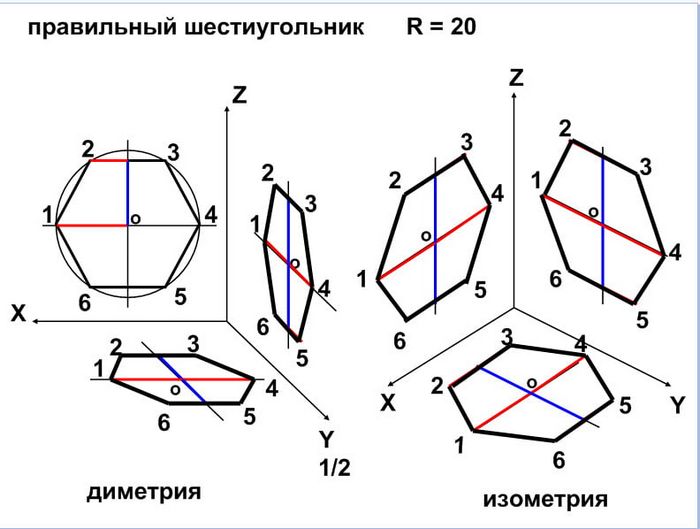
Пример 2. Построение аксонометрических проекций правильного шестиугольника.
Шести-угольник вписывают в окружность, разделив окружность на шесть одинаковых частей радиусом окружности.
Шестиугольник лежит на фронтальной плоскости (рис. 68).
Рис.
68. Шестиугольник на фронтальной плоскости
По оси ОХ откладуют радиусы описанной окружности, равные стороне шестиугольника из точки О влево и вправо.
По оси ОZ из точки О откладуют отрезки, равные половине расстояния между противоположными сторонами шестиугольника вниз и вверх, размер S.
Через полученные точки на оси ОZ проводят линии, параллельные оси ОХ, и из точки пересекания откладуют на них отрезки, равные половине стороны шестиугольника.
Полученные шесть точек объединяют.
Шестиугольник находится на горизонтальной поверхности (рис. 69).
Рис. 69.
Шестиугольник на горизонтальной поверхности
Построение выполняют так, как было рассмотрено, с той лишь разницей, что размер S между противоположными сторонами для диметрии берут меньше практически вдвое.
Шестиугольник находится на профильной плоскости (рис.
70).
Рис.
70. Шестиугольник на профильной плоскости
В данном случае размер, равный диаметру и размер, равный стороне шестиугольника берут меньше практически вдвое для диметрии.
Окружность в изометрии
Окружность в изометрии собой представляет замкнутую кривую линию, которая именуется эллипсом. Эллипсы строить тяжело, благодаря этому на практике черчения взамен них возводят овалы.
Овал – закрытая циркульная кривая, очерченная дугами окружностей. Овал комфортно строить, вписывая в ромб, являющийся изометрической проекцией квадрата.
Рассмотрим пример построения окружности в изометрии, лежащей на горизонтальной поверхности(рис. 71).
Рис.
71. Построение окружности в изометрии
Чтобы построить овал нужно найти точки, принадлежащие овалу и точки, из которых проводят дуги окружности.
Откладываем по осям ОХ и ОY размер, равный диаметру заданной окружности, строим ромб.
Делим стороны ромба надвое и через полученные точки нужно провести линии, параллельные осям ОХ и ОY, точки 1,2,3,4 будут принадлежать овалу.
Находим точки, из которых будем проводить дуги окружности, две точки (а, в) есть уже, еще две точки (с, d) лежат на большей диагонали ромба.
Проводим большую диагональ, объединяем точку 1 и точку 2 с точкой в.
Точки пересекания проведенных линий с большей диагональю есть точки с и d.
Строим овал, для этого из точек а и в радиусом, равным а3 проводим дуги, потом из точек с и d, радиусом с1 еще две дуги, приобретаем овал.
Овалы, расположенные на фронтальной и профильной плоскостях, возводят также (рис. 72).
Рис. 72.
Построение овалов, размещенных на фронтальной и профильной плоскостях
Из рассмотренных аксонометрических проекций огромным преимуществом пользуется изометрия, благодаря этому в последующем будем проводить построение геометрических тел и деталей только в изометрии.
Вы уже знаете, что форма любого предмета это комбинирование геометрических тел или их частей.
В основании каждого геометрического тела лежит конкретная фигура. Выстроив фигуру основания в необходимой плоскости, можно не прилагая больших усилий достроить ее до геометрического тела.
Пример 1. Построение параллелепипеда в изометрии.
1. Строим чертеж параллелепипеда в трех видах.
2. Построение параллелепипеда в изометрии начнем с нижнего основания, откладываем по оси ОХ- длину, а по оси ОY- ширину, достраиваем изометрическую проекцию прямоугольника, потом из вершин прямоугольника нужно провести линии параллельно оси ОZ, откладываем высоту, объединяем точки и определяем видимость граней (рис.
73).
Рис. 73.
Чертеж параллелепипеда в трех видах и изометрии
Пример 2. Построение шестиугольной призмы в изометрии.
1. Строим чертеж призмы в трех видах.
2. Построение начнем с нижнего основания.
Строим шестиугольник в изометрии на плоскости Н, потом из вершин шестиугольника нужно провести линии параллельно оси О Z и на них откладываем высоту, объединяем точки и определяем видимость граней (рис. 74).
Рис. 74.
Чертеж призмы в трех видах и изометрии
Пример 3. Построение четырехугольной пирамиды в изометрии.
1. Строим чертеж пирамиды в трех видах.
2. Построение начнем с нижнего основания, потом из центра основания проводим линию параллельно оси ОZ, откладываем высоту пирамиды, объединяем полученные точки и определяем видимость граней (рис. 75).
Рис.
75. Чертеж пирамиды в трех видах и изометрия
Пример 4. Построение цилиндра в изометрии.
1. Строим чертеж цилиндра в трех видах. Построение начнем с нижнего основания.
Сечение и разрез
2. Строим овал и из центра овала проводим линию параллельно оси ОZ, через получившуюся точку нужно провести линии, параллельно осям ОХ и ОY.
3. Строим овал (верхнее основание), объединяем верхнее основание касательными линиями с нижним Основанием (рис. 76).
Рис.
76. Чертеж цилиндра в трех видах и изометрия
Пример 5. Построение детали в изометрии по чертежу (рис. 77).
Рис. 77.
Чертеж детали в 2-х видах и изометрия
1. Анализируем геометрическую форму детали по чертежу, определяем симметричность.
2. Построение начнем с нижнего основания, строим параллелепипед.
3. Находим центр верхнего основания параллелепипеда, через центр нужно провести линии параллельно осям ОХ и ОY.
4. Строим меньший параллелепипед, определяем видимость граней.
Построение аксонометрической проекции детали от ее нижнего основания считается многофункциональным и применяется для построения деталей самой разной сложности.
Аксонометрические проекции
В большинстве случаев при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения подобных изображений используются проекции, именуемые аксонометрическими .
Способ аксонометрического проецирования заключается в том, что этот предмет одновременно с осями прямоугольных координат, к которым данная система относится в пространстве, параллельно проецируется на определенную поверхность ? (Рисунок 4.1).
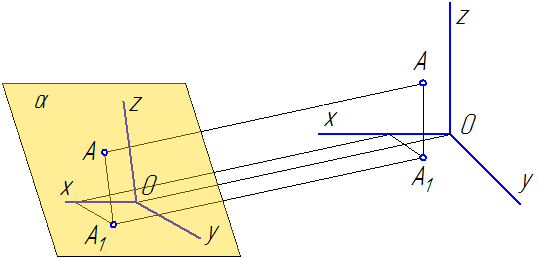
Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций ?, а еще коэффициенты искажения по ним.
При этом требуется обеспечить наглядность изображения и возможность делать определения положений и размеров предмета.
Как пример на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2
Тут буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ исходя из этого. Если все три коэффициента равны между собой, то аксонометрическая проекция именуется изометрической, если равны между собой всего лишь два коэффициента, то проекция именуется диметрической, если же k?m?n, то проекция именуется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций ?, то аксонометрическая проекция называется квадратной.
В другом случае, аксонометрическая проекция именуется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие с прямыми углами и косоугольные аксонометрические проекции:
- с прямыми углами изометрические и диметрические;
- косоугольные фронтально изометрические, в горизонтальном положении изометрические и фронтально диметрические;
Ниже приводятся параметры только трех очень часто применяемых В практических условиях аксонометрических проекций.
Любая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, размещенных в плоскостях, параллельных координатным поверхностям. Для упрощения геометрических построений коэффициенты искажения по осям, в основном, округляются.
4.1. С прямыми углами проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
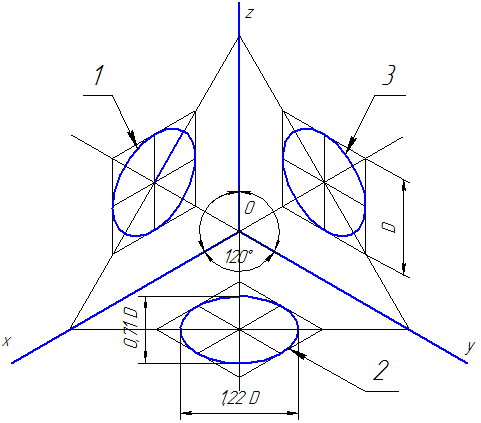
Рисунок 4.3 – Аксонометрические оси в квадратной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с подобными значениями коэффициентов искажения работать не комфортно, благодаря этому, В практических условиях, применяются приведенные коэффициенты искажений.
Эта проекция в большинстве случаев делается без искажения, благодаря этому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных поверхностям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а небольшая – 0,71 диаметра создающей окружности D.
Большие оси эллипсов 1, 2 и 3 размещены под угол 90? к осям OY, OZ и OX, исходя из этого.
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в квадратной изометрической проекции
4.1.2. Диметрическая проекция
Положение аксонометрических осей проходит на Рисунке 4.5.
Для построения угла, примерно равного 7?10?
, выстраивается прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, примерно равного 41?25?
— катеты треугольника, исходя из этого, равны семи и восьми единицам длины.
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47.
При округлении таких параметров принимается k=n=1 и m=0,5.
В данном случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 размещены под угол 90?
к осям OY, OZ и OX, исходя из этого.
Пример квадратной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в квадратной диметрической проекции

Рисунок 4.6 – Изображение детали в квадратной диметрической проекции
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на Рисунке 4.7. Разрешается использовать фронтальные диметрические проекции с наклонным углом к оси OY, равным 30 0 и 60 0 .
Показатель искажения по оси OY равён m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на поверхность XOZ без искажения.
Большие оси эллипсов 2 и 3 равны 1,07D, а небольшая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7?
14?, а большая ось эллипса 3 составляет аналогичный угол с осью OZ.
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, эта деталь размещается поэтому, чтобы её окружности проецировались на поверхность XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из данных окружностей разделяется на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые разделяют также вторую окружность. Потом через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересекания надлежащих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана только одна необходимая точка 1.
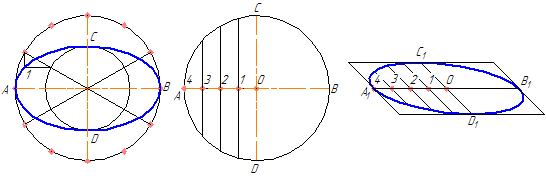
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ разделяется на несколько одинаковых частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (к примеру, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения.
Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 разделяется на то же число одинаковых частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, помноженным на показатель искажение (в нашем случае – 0,5).
4.4 Штриховка сечений
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в надлежащих координатных плоскостях, их стороны параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в квадратной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Варианты штриховки в аксонометрических проекциях