Разница между квадратом и прямоугольником

Разница между квадратом и прямоугольником

Четырехугольником именуют многоугольник, у которого 4-ре вершины и 4-ре стороны.
Иначе можно сказать, что четырёхугольником считается фигура геометрической формы в виде многоугольника, который имеет только 4-ре угла.

Любой предмет или устройство, которое имеет такую форму также можно назвать четырехугольником. Две стороны четырехугольника, которые в отношении друг к другу являются несмежными, называются противоположными.

Два угла и две вершины, которые не считаются соседними, именуют противоположными.
Четырехугольник формируют, как параллелограмм, если у него противолежащие стороны попарно параллельны.

Обозначение

Квадрат — это параллелограмм, у которого все 4-ре стороны равны и все 4-ре угла прямые.
Прямоугольник — это параллелограмм, у которого противолежащие стороны, которые параллельны друг дружке, равны и все углы прямые.

Сравнение

Квадратом именуют параллелограмм, у которого все 4-ре внутренних угла прямые. Все 4-ре стороны квадрата равны, другими словами имеют одинаковую длину.

Прямоугольником именуют параллелограмм, внутренние углы у которого прямые, и только разные стороны, которые параллельны друг дружке, равны.
Для прямоугольника и квадрата свойственны следующие свойства:

• все углы прямые;
• диагонали равны;
• в точке пересекания диагонали разделяются на двое;
• противолежащие стороны параллельны друг дружке и равны по длине.

Квадрат считается прямоугольником

Добрый вечер!
Помогите мне разобраться, пожалуйста, с одной темой по геометрии, по ходу, я её не очень поняла, а теперь появляются проблемы. Смотрите, у меня есть квадрат и прямоугольник. Так вот можно ли сказать, что квадрат считается прямоугольником либо нет? а то я как-то запуталась
Доброй ночи!
Эта тема относится к четырёхугольником, который, со своей стороны, именуют многоугольником, 4-ре вершины и 4-ре стороны которого равны.
Говоря иначе, мы можем сказать, что четырёхугольником считается такая фигура геометрической формы, имеющую вид многоугольника, содержащего только лишь 4-ре угла. Любой предмет, у которого такая форма, можно назвать четырехугольником.
Теперь я предлагаю остановится конкретнее на понятиях квадрат и прямоугольник, чтобы понять квадрат считается прямоугольником либо нет!
Квадрат – это такой параллелограмм, у которого все 4-ре стороны равны и все 4-ре угла прямые (другими словами равны 90 градусам).
А прямоугольник, со своей стороны, — это параллелограмм, у которого противолежащие стороны, которые параллельны друг дружке, равны и все углы прямые.
Однако сейчас важно усвоить, в чем же всё-таки разница между квадратом и прямоугольником. Для этого мы будем рассматривать, что отличительно для данных фигур геометрической формы.
Для прямоугольника и квадрата свойственны подобные характеристики:

• все углы прямые;
• диагонали равны;
• в точке пересекания диагонали разделяются на двое;
• противолежащие стороны параллельны друг дружке и равны

А отличие квадрата от прямоугольника состоит в следующем:

Геометрия 8 класс (Урок№6 — Прямоугольник. Ромб. Квадрат.)

1. В квадрате все 4-ре стороны равны.
2. В прямоугольнике только разные стороны, которые параллельны друг дружке, равны.

Надеюсь, сейчас вам стало более ясно, что это и как! Удачи!

Пожалуйста, пройдите регистрацию или войдите, чтобы добавить ответ.

Копирование материалов с сайта может быть только с согласия
администрации портала и при наличие активной ссылки на источник.

Квадрат (прямоугольник)

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Смотреть что такое "Квадрат (прямоугольник)" в прочих словарях:

КВАДРАТ — • КВАДРАТ, в биологии квадратная рама, применяемая для размечивания участка поверхности с целью изучения растений, присутствующих на нем. Квадратом именуют также и сам данный участок почвы.

8 класс, 8 урок, Ромб и квадрат

В основном, такой квадрат равён 0,5 или 1 м2. Пользуясь этим… … Научно-технический энциклопедический словарь

Прямоугольник — [rectangle]: Смотри также: прямоугольник квадрат прямоугольник гладкая бочка … Энциклопедический словарь по металлургии
КВАДРАТ — (лат. quadratum, от quadrare сделать прямоуголным).

1) прямоугольный, равносторонний четырехугольник. 2) такое число, которое, будучи умножено само на себя, даёт данное число.

3) единица чтобы провести измерения плоскостей; напр.: квадратн. фут, дюйм и… … Словарь зарубежных слов русского языка
Прямоугольник — Прямоугольник параллелограмм, у которого все углы прямые (равны 90 градусам).

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!

Примечание.

В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу … Википедия

прямоугольник — параллелограмм, четырехугольник, квадрат Словарь русских синонимов. прямоугольник сущ., кол во синонимов: 4 • квадрат (9) • … Словарь синонимов
квадрат — параллелограмм, клетка, материал, прямоугольник, степень, квадратик Словарь русских синонимов. квадрат сущ., кол во синонимов: 9 • гиперкуб (12) • … Словарь синонимов

КВАДРАТ — КВАДРАТ, квадрата, супруг. (лат. quadratus прямоуголный). 1. Равносторонний прямоугольник (мат.).

2. Форма такого прямоугольника у какого нибудь предмета (книжн.).

Ярко освещенный квадрат окна. 3. Прямоуголный гартовый брусок мера для… … Толковый словарь Ушакова

КВАДРАТ — (от латинского quadratus прямоуголный), 1) равносторонний прямоугольник.

2) Вторая степень a2 числа a (наименование с тем связано, что собственно так выражается площадь квадрата со стороной a) … Современная энциклопедия
КВАДРАТ — (от лат. quadratus прямоуголный) 1) прямоугольник с равными сторонами.2) Вторая степень числа (а), другими словами а?а = а2 … Большой Энциклопедический словарь

Геометрия 8. Урок 2 — Параллелограмм. Свойства и признаки.

КВАДРАТ — КВАДРАТ, а, супруг. 1. Равносторонний прямоугольник, а еще предмет или участок этой формы.

Квадраты на шахматной доске.

Взлётный к. для вертолётов. 2. В математике: творение числа на самого себя.

Четыреэто к. 2-ух.

3. В математике: критерий … Толковый словарь Ожегова

Прямоугольник и квадрат

Обозначение
Прямоугольник – это параллелограмм, у которого один угол прямой.
Аналогичным образом, прямоугольник обладает всеми характеристиками параллелограмма:
\(\sim\) разные стороны попарно равны;
\(\sim\) диагонали точкой пересекания разделяются на двое.
Теоремы: свойства прямоугольника
1) Все углы прямоугольника прямые.
2) Диагонали прямоугольника равны.
Подтверждение
1) Пускай \(\angle A=90^\circ\) . Т.к. в параллелограмме сумма соседних углов равна \(180^\circ\) , то \(\angle B=180^\circ-\angle A=90^\circ\) .
Т.к. в параллелограмме противоположные углы равны, то \(\angle C=\angle A=90^\circ, \angle D=\angle B=90^\circ\) , чтд.
2) Рассмотрим прямоугольник \(ABCD\) .

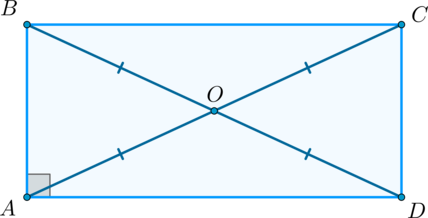
С прямыми углами треугольники \(ACD\) и \(DBA\) равны по двум катетам ( \(CD = BA\) , \(AD\) – общий катет). Отсюда следует, что гипотенузы данных треугольников равны, т.е. \(AC = BD\) .
Аналогичным образом, половинки диагоналей в прямоугольнике равны, т.е. \(OA=OB=OC=OD\) .
Теоремы: признаки прямоугольника
1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
2) Если в выпуклом четырехугольнике все углы прямые, то он – прямоугольник.
Подтверждение
1) Пускай в параллелограмме \(ABCD\) диагонали равны.

Треугольники \(ABD\) и \(DCA\) равны по трем сторонам ( \(AB = CD\) , \(BD = AC\) , \(AD\) – общая сторона). Отсюда следует, что \(\angle A = \angle D\) . Так как в параллелограмме противоположные углы равны, то \(\angle A = \angle C\) и \(\angle B = \angle D\) . Аналогичным образом, \(\angle A = \angle B = \angle C = \angle D\) . Параллелограмм – выпуклый четырехугольник, благодаря этому \(\angle A + \angle B + \angle C + \angle D = 360^\circ\) . Поэтому, \(\angle A = \angle B = \angle C = \angle D = 90^\circ\) .
2) Рассмотрим четырехугольник \(ABCD\) :

Т.к. \(\angle A+\angle B=180^\circ\) – односторонние углы при прямых \(AD\) и \(BC\) и секущей \(AB\) , поэтому, \(AD\parallel BC\) .
Подобно доказывается, что \(AB\parallel CD\) . Значит, \(ABCD\) – параллелограмм. Т.к. у него более того все углы прямые, то по определению это прямоугольник.
Обозначение
Два равноценных определения квадрата:
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат – это ромб, у которого один угол прямой.
Свойства квадрата
Так как квадрат считается прямоугольником и ромбом, то он обладает всеми характеристиками прямоугольника и ромба:
\(\sim\) Все углы квадрата равны \(90^\circ\) ;
\(\sim\) Все стороны квадрата равны;
\(\sim\) Диагонали квадрата равны, обоюдно перпендикулярны, точкой пересекания разделяются на двое и разделяют углы квадрата надвое.